CENTER OF MASS OF FLAT FIGURES

We will indicate two ways to determine the center of mass of plates from their physical properties.

For the first, hang the figure on a peg. Then use the plumb line to mark a vertical line on the board. Repeat the process by hanging the plate in another position. There you are, the intersection of the two lines is the center of mass!

The second uses a metal plate to balance the figure in two different positions, marking the position of the metal plate. Again, the intersection of the lines is the center of mass!

A close-up of the metal plate used in the second method.

However, the center of mass can also be determined mathematically, based only on the shape of the plate (assuming it is homogeneous). For a triangular plate, for example, it is the meeting point of the medians, that is, the barycenter of the triangle. For a polygonal plate, it can be determined by decomposing the polygon into several triangles and then weighting the centers of mass of each by their areas.

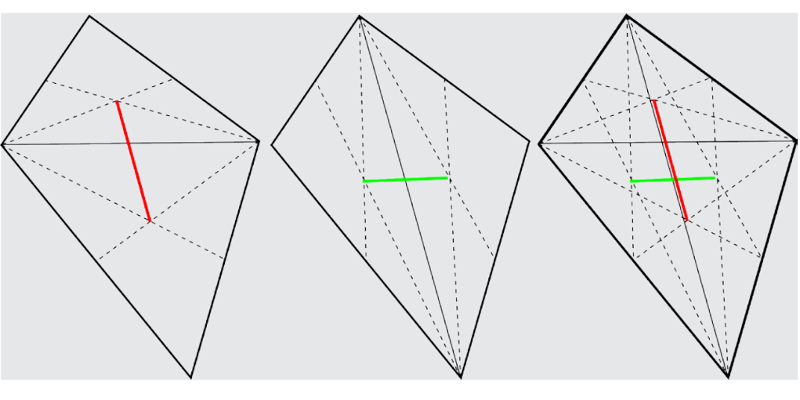
In the figure below we see 3 copies of a quadrilateral. In the first one, we divided it into two triangles and found their centroids by meeting two medians. The red segment between the two centroids must contain the plate's center of mass. We do the same with another division into triangles and from there we deduce that the center of mass is in the green segment. Conclusion: the center of mass is the intersection of the green and red segments.

USEFUL LINKS

This Wikipedia page talks about centers of mass, bringing a more "simple" and intuitive point of view, but also a more complex one, including concepts from higher education.


This Khan Academy article explains how to find the center of mass of plane figures, both experimentally and through calculations, also thinking about the union of pieces that form larger figures.

On this Caio Dallaqua channel video, the USP professor Dr Leonardo Paulo Maia talks about the center of mass from a more physical point of view, explaining which concepts are involved in a more elaborate calculation of the center of mass.

Very interesting are the experiments involving center of mass! This Anderson Almeida channel video shows the equilibrium of some objects from the support at this specific point. The same idea is used to make the birds in this Gênios da Física channel video balance!

Continuing with the experiments, this Galeradafisica channel video shows how the center of gravity and physical balances are the basis of many incredible experiments. During the video, the physics teacher explains how the concepts are applied at each moment.

As stated in the text, the center of mass of any triangle is at its centroid. To learn more about this and the other notable points of the triangle, this Brasil Escola page can help a lot, with succinct explanations and drawings that facilitate understanding.