GALTON BOX OR QUINCUX

This experiment serves, as a first approximation, to illustrate the so-called binomial distribution.

By placing the piece “upside down”, all the marbles will fall. See your distribution.

If on each peg the probability of going to the right or to the left is the same, the marbles below will be distributed proportionally to the coefficients of the expansion of (a + b)n, which is Newton's binomial (in the experiment, n = 9).

For example,
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
has coefficients 1, 4, 6, 4 and 1.

The coefficients of (a + b)n can be easily obtained on the nth line of Pascal's triangle (see figure below). Except at the ends, each number in a row is obtained as the sum of the two elements of the previous row that are closest to it.

Pascal's triangle up to n = 4.

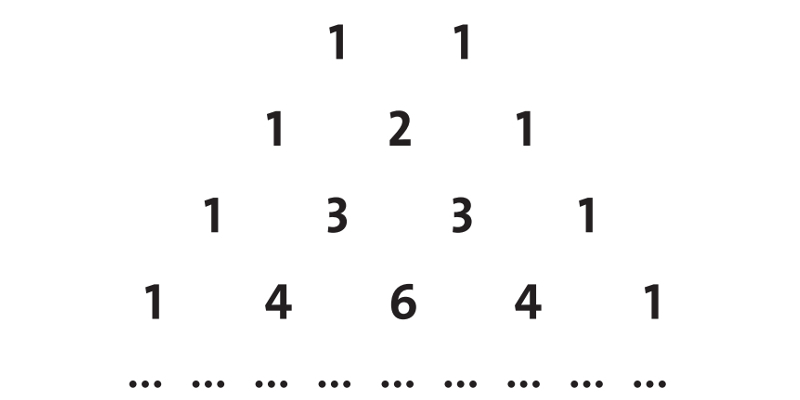
However, it is not difficult to notice that the parameters involved in the experiment, such as the radius of the pegs and marbles, the distance between the pegs, the elasticity of the shocks, etc., can influence the result (think, for example, that if the pegs were too apart, then all the balls would fall in the middle). This shows the need for more accurate modeling.

If you want to see a little more about this game, check out the video below! Enjoy and check out the other really cool videos on Matemateca's channel on YouTube!

                 

USEFUL LINKS

On this iMática page you will find more explanations about the binomial distribution, Pascal's triangle, and a Galton board simulator to play with!



This Wikipedia page talks about Galton's Board, also called Quincunx. In it, we have a description of the operation of the machine and the distribution of the balls, which has to do with the binomial distribution. There is also a brief commentary on its history.                                                          

This Four Pines Publishing's channel video is a documentary about the Galton Board and how it was built as an object to study the normal distribution, so present in most studies of quantitative variables. It is a very interactive video, with several images, comparisons and speeches by some scholars.

This Math is fun page allows internet users to simulate the Galton Board, being able to choose the size of the board, that is, the number of lines, which varies from 1 to 15, the speed of the balls and the probability of it going to the right or to the left . If the 50% / 50% setting is not changed, it is the original Board, as the probability is the same on a well-built board.

Finally, this article by a student at the State University of Campinas brings the study of the binomial distribution using the Galton Board. In it, there is a handmade assembly of the Board and a very in-depth study of probabilities, with more precise statistical concepts. Experimental results and a study of them and the uncertainties involved are presented.