PEAUCELLIER INVERSOR
In the 19th century, several scientists and engineers were interested in discovering mechanisms that would transform a rectilinear motion into a circular motion. This would be useful, for example, for locomotives with steam engines.
The French engineer and officer Charles-Nicolas Peaucellier, in 1864, was the first to invent such a mechanism that was exact - James Watt had invented another, which was used until then, but was approximate. It is this mechanism that we present here, in two ways. After all, as is often the case in science, this same mechanism was independently discovered in 1873 by the Lithuanian mathematician Yom Tov Lipman Lipkin.
The mathematical principle that Peaucellier explored was the inversion through a circle, which works similarly to a reflection in the plane by a line. The basic part of the mechanism makes two of its points the inverse of each other by this inversion.
Mechanism
The basic drive mechanism has 6 articulated bars, two H-size and four H-size. The larger ones meet at a point fixed to the board (O), with their opposite ends articulated with opposite vertices of the rhombus formed by the four smaller ones. The idea is to make point P walk on a curve and follow what point Q does.
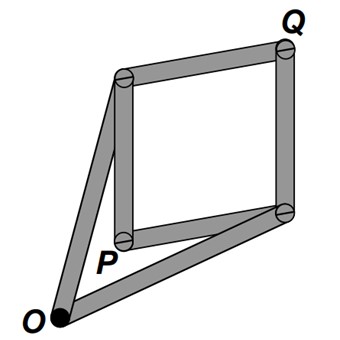
What the mechanism is doing is what is called an inversion through the circle of radius r. The inversion image of P is the point Q, and vice versa. In an inversion operation, a point and its image lie on the same ray and the geometric mean of their distances from the origin is equal to the radius of the circle.
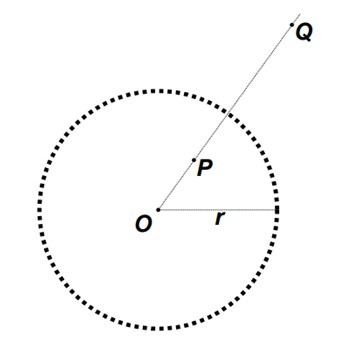
Inversion
Generally speaking, the inversion of a circle is still a circle. An example is illustrated in the first part. The exception occurs when the circle passes through the origin: in this case, the inversion of this circle is a straight line. The second piece illustrates this: point P is forced to traverse a circle segment that passes through the origin. This causes point Q to automatically traverse a line segment. That was exactly Peaucellier's proposal to transform rectilinear movements into circular ones, and vice versa.
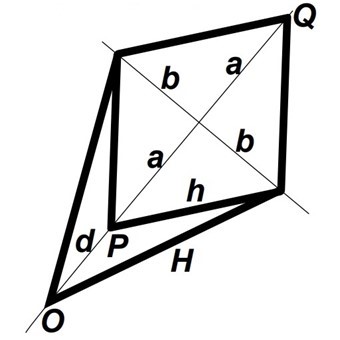
If d = OP and D = d + 2a = OQ, we can conclude, using the Pythagorean Theorem twice, that, regardless of the angles of the joints, it always holds d x D = H2 - h2. If r is such that r2 = H2 - h2, then the distances from P to O and from Q to O have a geometric mean equal to r. Just think of the situation where P coincides with Q.
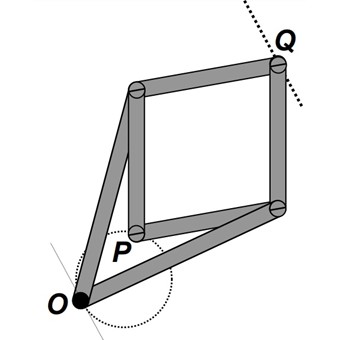
By constraining that point P only moves through a circle that passes through O, point Q automatically traverses a straight line. This line is parallel to the tangent line to the circle on which P is constrained, at point O.
Image: Rodrigo Tetsuo Argenton.
