The citizens of Königsberg (today Kaliningrad, Russia) wondered if it was possible to take a walk through the city passing exactly once on each of its (at the time) seven bridges.

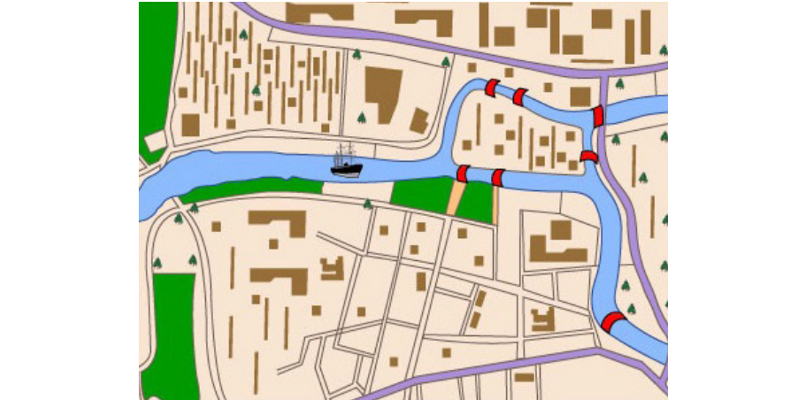
Leonard Euler, a great Swiss mathematician, gave a simple and elegant solution to the matter. To do so, he "translated" the problem into the graph language. Many consider this result, published in 1736, the first paper in Graph Theory. A graph is a set of points (vertices) linked (or not) by one or more dashes (edges).

The original problem of the Konigsberg Bridges, illustrated above, has no solution. Note that for the path to pass exactly once on each bridge, the portions of land where the walk starts and ends are the only ones that can have an odd number of bridges.

Currently, this theory arouses great interest for its many applications: electrical circuits, logistics, administration of networks, etc. For example, a telephone network or the internet can be treated as graphs.

Place as many bridges as you like connecting the regions and then try, with the chalk, to draw a path that goes through all the bridges without repeating any! There is no need to go back to the starting point. Not always does this problem have a solution. What does the existence of a solution depend on?