TAUTOCHRONE
One of the intriguing properties of this ramp is the fact that if two marbles are dropped from different positions, they will eventually reach the lowest point at the same time. That is why the curve is called tautochrone, from the Greek “tautos” (same) with “chronos” (time).


Note that this is a rare property in oscillatory motions. For example, in a simple pendulum the period of oscillation increases with amplitude. That's why this curve seemed interesting for making clock pendulums. In practice, friction ended up eliminating the apparent technical advantage.
Another property of this curve is that it makes the best use of gravity: to go from the highest point of the ramp to any point, the shortest time is given if the ball goes down this curve. For this reason, it is also called brachistochrone, as “braquis” means “short” in Greek.
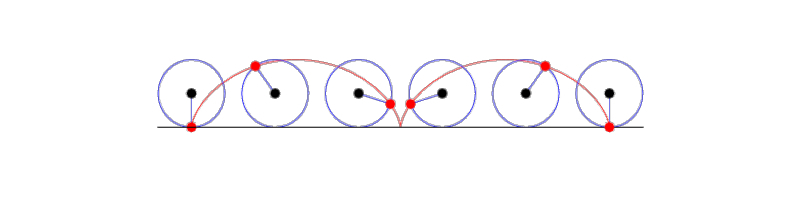
A cycloid is a curve traced by a point on the edge of a circle rolling in a straight line on a flat surface. As if we painted a red circle on a bicycle wheel. The red ramp has this shape (it's upside down).
You can see how they actually make it to the middle at the same time by watching the two gifs below. Note that, although the two marbles start in very different places, this is irrelevant on their arrival.


