In the secret santa raffle with N people, some draws are viable (no person gets their own name) and others are not. This naturally raises questions like: how likely is a secret santa raffle to be viable?
If the number of people is N, the probability of a draw being viable is given by the formula:
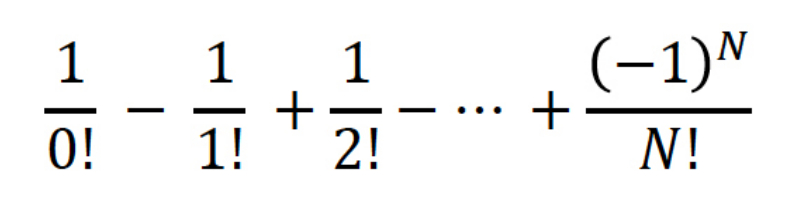
When the number of people tends to infinity, this probability tends to 1⁄e = 0.367879…
A challenge: what is the probability that exactly one person takes their own name?
The concept of probability is very present in the analysis of this piece. This Wikipedia page discusses this subject, approaching related concepts, interpretations and applications of Probability Theory in everyday life.
This RPM's (Mathematics Teacher Magazine) article addresses the secret santa raffle problem, using concepts such as chaotic permutation and the idea of recurrence to answer the questions presented on this page, like the ones that led to the formula above.
Finally, the Todas as Configurações Possíveis (All Possible Settings) it also introduces the secret santa raffle problem, but with more specific questions, such as the probability of someone taking themselves out or the probability of forming a complete cycle with the players.