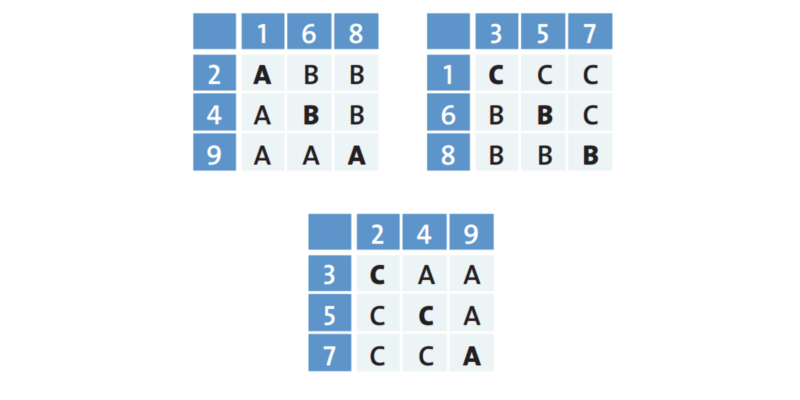
INTRANSITIVE DICES

Which dice is more likely to win in a head-to-head match: A (2-4-9), B (1-6-8), or C (3-5-7)?

If A beats B and B beats C, can we conclude that A beats C?

Despite seeming “reasonable”, we have many examples where this does not occur. One of them is the game of “joquempô” (rock-paper-scissors). Football also provides examples: in the Brazilian championships from 2009 to 2013, São Paulo beat Atlético 6 times and lost 3; Atlético won 4 from Fluminense and lost 3; and Fluminense won 5 against São Paulo and lost 3. Who was the best among the three?

Here the example is with this data. To verify this, see the possibilities of results in two-by-two plays in the tables to the side. What fails in this data is the transitive property. This seems bizarre because we have this property built into our reasoning. In real numbers, for example, if x < y and y < z then x < z.

The first two tables show that A is better than B, and B is better than C. Need the third table?

USEFUL LINKS

This RPM (Mathematics Teacher Magazine) article explains the idea of these non-transitive data, in addition to showing some other particular cases and their results. A bonus: this article was written by Professor Deborah Rafael, member of Matemateca!

This Wikipedia page also talks about non-transitive data, giving a more theoretical and statistical view of these data. The page is in English, but there are many examples, accounts and tables of reasonable understanding, including the analysis of data with 12 faces!

This SAS (Analytics Software & Solutions) page explains non-transitive data using probability trees, as well as offering programming code that allows you to simulate the results in a non-transitive game.                                                                                       

Since we are talking about non-transitive relationships, it is important to understand what transitive relations are. This Wikipedia page explains what this relation is, in addition to showing its properties in a slightly more formal way.

The study of non-transitive data makes a lot of use of double-entry tables. To understand them better, this Khan Academy's set of videos and articles has a lot of information on how to use and interpret various tables like these.