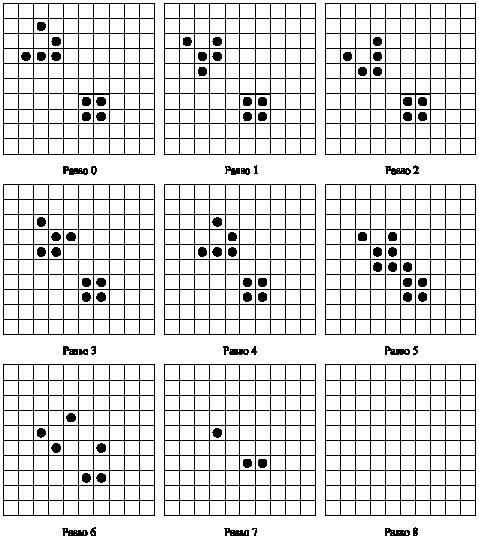
In this exhibit, in each cycle, the LEDs that are lit are read and it is decided which ones will be lit in the next cycle, according to a rule: “a LED will be lit in the next cycle if exactly 4 of its neighbors were lit in the previous cycle” .

The initial condition is chosen by lot. Every time the LED pattern reaches a steady state (everything off, for example), a new initial condition is drawn. Otherwise, the process stops after a certain number of iterations.

This is an adaptation of the famous Game of Life created by John Horton Conway in 1970, which features stationary, periodic, self-replicating patterns and a whole fauna of phenomena that justifies its name. It belongs to a broad class of dynamic systems called cellular automata.

In Conway's Game of Life, the rule is slightly different from the one we programmed in the 3D version: an unlit cell lights up if it has exactly 3 neighboring cells (out of the possible 8) lit. And a lit cell only stays lit if it has exactly 3 or 4 neighboring cells lit.

In this version, exploited to exhaustion by thousands of people, anything happens! In the next image, you can see a sequence of steps in which the stable configuration of four lights (the little square) is destroyed by a block of lights that "shifts".