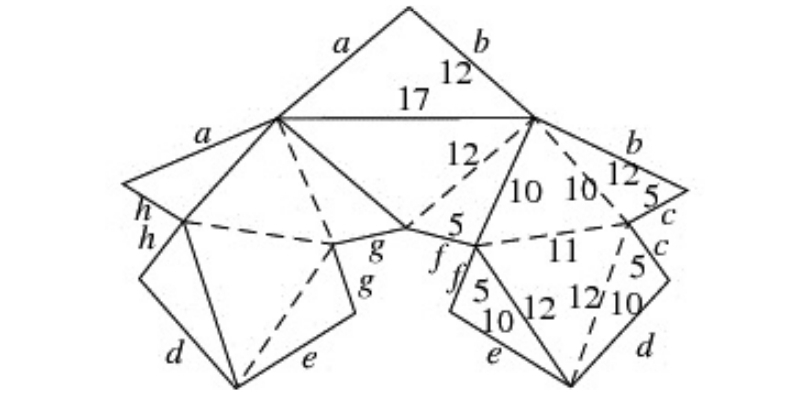
FLEXIBLE POLYHEDRA
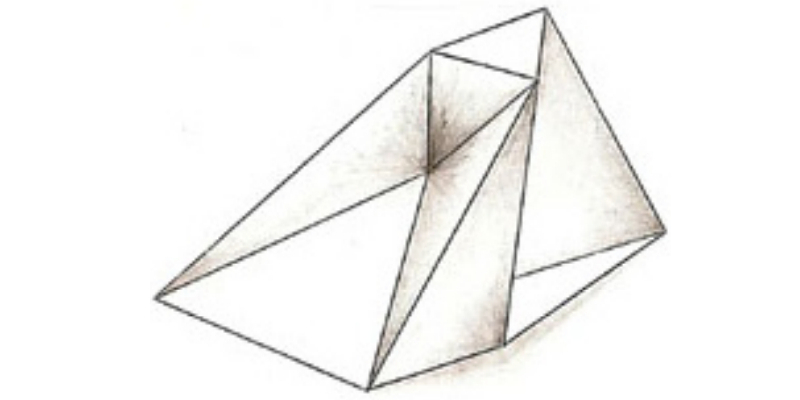
The polyhedron appearing in the picture is flexible!! The faces are rigid and the edges flex as if they were hinges.
This may not be surprising at first glance, but it is a recent achievement of geometry. In 1813, Cauchy proved that a convex polyhedron can not be flexible, but the question remained whether this would be possible with non-convex polyhedra.
It was only in 1977 that Robert Conelly found the first example of a non-convex and flexible polyhedron. The object we presented here was created by Klaus Steffen a few years later.
A problem recently solved was the so-called “bellows conjecture”: it was speculated that a flexible polyhedron should have a constant volume. The positive answer to this conjecture was given by Conelly in 1997. In concrete terms, it means that if we open a hole in one face, the movement of the polyhedron neither expels nor sucks air, hence the name of the conjecture.