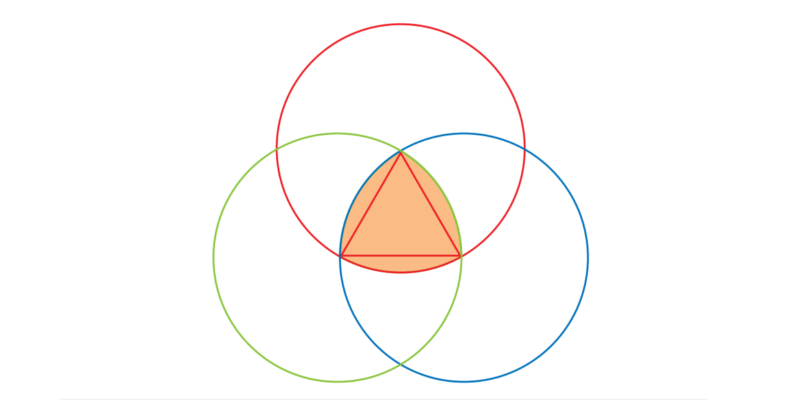
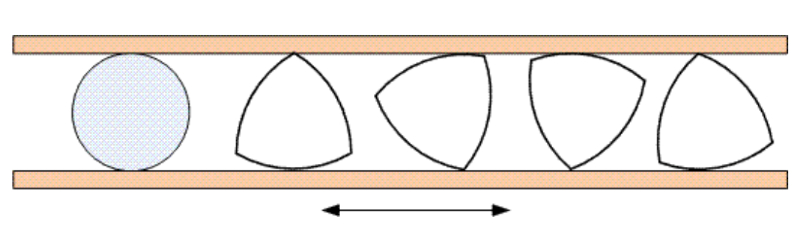
REULEAUX TRIANGLE

A constant width flat shape has the following property: whenever two parallel lines just touch the shape enclosing it, the distance between the lines is constant. Besides the circle, the simplest example is the Reuleaux triangle, which we present here.

The figure above illustrates how the Reuleaux triangle is constructed: all circles have the same radius.
The 50 pence English coin is constructed from a regular heptagon and has constant width.

USEFUL LINKS

This Wikipedia page talks about the Reuleaux triangle, also called the spherical triangle. There is an explanation of how it can be constructed using a rule and a compass, but also a brief comment on how to round the sides of an equilateral triangle.                                                                                                                                                                                 

This Atractor page also talks about the construction of the Reuleaux triangle, in a way more analogous to what was mentioned on this page. In addition, there is some more precise information about the measurements involved in such a process, such as the relation between the side of the equilateral triangle and the radius of the circle.

This José Luiz Pastore Mello's article, found in RPM 81 (Mathematics Teacher Magazine), talks about Reuleaux polygons, giving several examples of everyday objects where this type of figure is found and bringing some exercises with curves of constant diameter. Finally, it brings a generalization of pi to other figures other than the circle.

In one of the exercises in the previous link, there was a request for the construction of the Reuleaux triangle with a ruler and compass. This Sérgio Dantas' article comes, in response to the RPM article, to add a proposal for building Reuleaux polygons using GeoGebra. The step by step is described throughout the text.

An interesting topic to be addressed is constant width curves. This Wikipedia page brings definitions, examples, constructions, properties and applications, in addition to some very interesting generalizations that can be carried out, including with regard to non-convex figures.                                                           

This another Atractor page also talks about the meaning of having constant width (and the consequences of this fact), starting from a simple example from everyday life: the wheels of a car. To complete, this Dinamática's page brings the animation of a star-shaped Reuleaux polygon.