INVERSOR DE PEAUCELLIER
No século XIX, vários cientistas e engenheiros estavam interessados em descobrir mecanismos que transformassem um movimento retilíneo num movimento circular. Isso seria útil, por exemplo, para as locomotivas com máquinas a vapor.
O engenheiro e oficial francês Charles-Nicolas Peaucellier, em 1864, foi o primeiro a inventar um tal mecanismo que fosse exato - James Watt havia inventado outro, que era usado até então, mas era aproximado. É este mecanismo que apresentamos aqui, de duas maneiras. Afinal, como frequentemente acontece em ciência, esse mesmo mecanismo foi descoberto de forma independente, em 1873, pelo matemático lituano Yom Tov Lipman Lipkin.
O princípio matemático que Peaucellier explorou foi a inversão por um círculo, que funciona de maneira semelhante a uma reflexão no plano por uma reta. A parte básica do mecanismo faz com que dois de seus pontos sejam o inverso um do outro por essa inversão.
Mecanismo
O mecanismo básico do inversor tem 6 barras articuladas, duas de tamanho H e quatro de tamanho h. As maiores se encontram em um ponto fixado à tábua (O), com suas pontas opostas articuladas com vértices opostos do losango formado pelas quatro menores. A ideia é fazer o ponto P andar sobre uma curva e acompanhar o que faz o ponto Q.
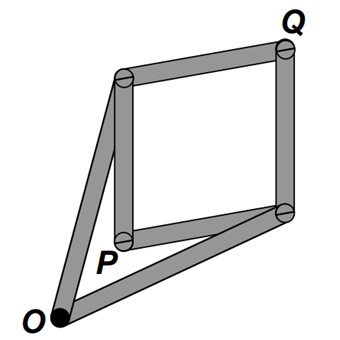
O que o mecanismo está fazendo é o que se chama uma inversão pelo círculo de raio r. A imagem de P pela inversão é o ponto Q, e vice-versa. Em uma operação de inversão, um ponto e sua imagem estão sobre a mesma semirreta e a média geométrica de suas distâncias à origem é igual ao raio do círculo.
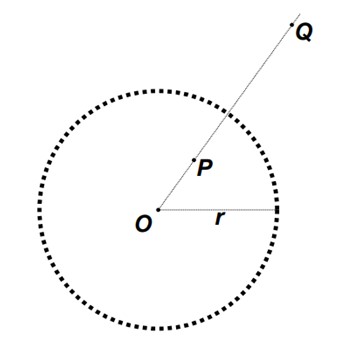
Inversão
De modo geral, a inversão de um círculo ainda é um círculo. Um exemplo está ilustrado na primeira peça. A exceção ocorre quando o círculo passa pela origem: neste caso, a inversão desse círculo é uma reta. A segunda peça ilustra isso: o ponto P é forçado a percorrer um segmento de círculo que passa pela origem. Isto faz com que o ponto Q percorra, automaticamente, um segmento de reta. Foi exatamente essa a proposta de Peaucellier para transformar movimentos retilíneos em circulares, e vice-versa.
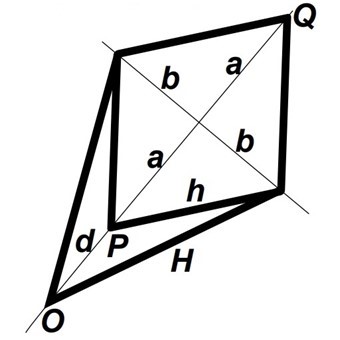
Se d = OP e D = d + 2a = OQ, podemos concluir, usando o Teorema de Pitágoras duas vezes, que, independentemente dos ângulos das articulações, sempre vale d x D = H2 - h2. Se r é tal que r2 = H2 - h2, então as distâncias de P a O e de Q a O têm média geométrica igual a r. Basta pensar na situação em que P coincide com Q.
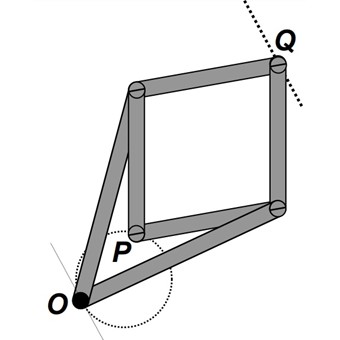
Ao restringir que o ponto P só se movimente por um círculo que passa por O, o ponto Q automaticamente percorre uma reta. Essa reta é paralela à reta tangente ao círculo sobre o qual P está restrito, no ponto O.
Imagem: Rodrigo Tetsuo Argenton.
