O JOGO "HEX"
O jogo Hex foi inventado de forma independente pelo matemático sueco Piet Hein e pelo matemático norte-americano John Nash (foto), aquele que se tornou conhecido por ter sua vida contada no filme “Mente brilhante”.
Parece incrível, mas neste jogo não há empate possível!
Em 2003, Jing Yang, Simon Liao and Mirek Pawlak encontraram uma estratégia vencedora para o primeiro jogador para tabuleiros de tamanho, 7X7, 8X8 e 9X9. Ainda se procura uma solução para o caso geral. Topa uma partida?

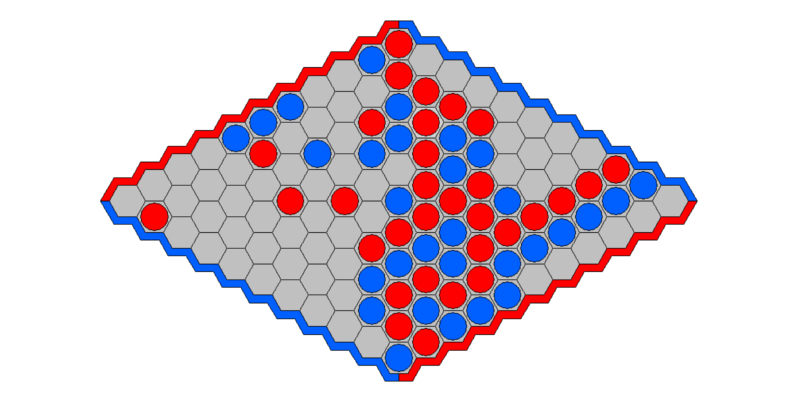
Atenção: Para formar o caminho não é preciso tê-lo sempre conectado, basta que ele se forme no final. Pode-se começar, por exemplo, com peças dos dois lados e fechá-lo no meio. Neste tabuleiro, as peças vermelhas ganharam. Você enxerga o caminho?

Nas próximas imagens, fotografadas por Rodrigo Tetsuo Argenton, temos um exemplo de uma partida do Hex! Você faria os mesmos movimentos ou conhece uma estratégia melhor? Consegue identificar claramente o caminho do vencedor?










































