Observe que essa é uma propriedade rara em movimentos oscilatórios. Por exemplo, no pêndulo simples o período de oscilação aumenta com a amplitude. Por isso essa curva parecia interessante para a confecção de pêndulos para relógios. Na prática, o atrito acabou por eliminar a aparente vantagem técnica.

Outra propriedade dessa curva é que ela é a que melhor “aproveita” a gravidade: para ir da ponta mais alta da rampa até qualquer ponto, o tempo mais curto se dá se a bolinha descer por essa curva. Por isso, ela também recebe o nome de braquistócrona, já que “braquis” significa “curto” em grego.

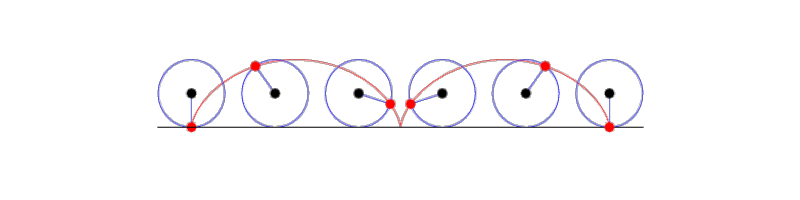
A cicloide é a curva traçada por um ponto do bordo de uma circunferência rolando em linha reta sobre uma superfície plana. Como se pintássemos um círculo vermelho numa roda de bicicleta. A rampa vermelha tem essa forma (está de cabeça para baixo).