A classificação das superfícies foi feita no século XIX: duas superfícies conexas, fechadas e limitadas são equivalentes se, e somente se, tiverem o mesmo número de componentes de bordo, orientabilidade e característica de Euler (ver abaixo). Essas três informações determinam completamente de que superfície se trata. De outra forma, duas superfícies são equivalentes se uma puder ser transformada na outra por meio de deformações sem rompimento, ou ainda, deformações com rompimento seguidas de “colagem de volta no mesmo lugar”.

A superfície esmaltada de uma xícara e um toro (que é o formato da câmara de pneu) são equivalentes nesse sentido, pois podemos deformar, ao menos imaginariamente, uma na outra. Um poliedro convexo pode ser deformado para se transformar numa esfera, e assim por diante.

Algumas superfícies, como a faixa de Möbius, têm bordo, enquanto outras, como a garrafa de Klein, não. O bordo constitui-se de uma ou mais curvas fechadas simples no espaço, formando nós ou enlaces.

As superfícies também podem ter “dois lados” (orientáveis) ou “apenas um lado” (não orientáveis). Você pode investigar isso passeando com o dedo por elas. Note que, se der apenas uma volta, seu dedo não volta ao mesmo lugar!

Essas peças, que lembram objetos artísticos ou de artesanato, ilustram uma área específica da Topologia, que é a Topologia Algébrica. Nessa teoria, as superfícies são vistas por suas propriedades mais intrínsecas, que não variam sob deformações, diferentemente da Geometria, que se preocupa com a forma exata dos objetos no espaço.

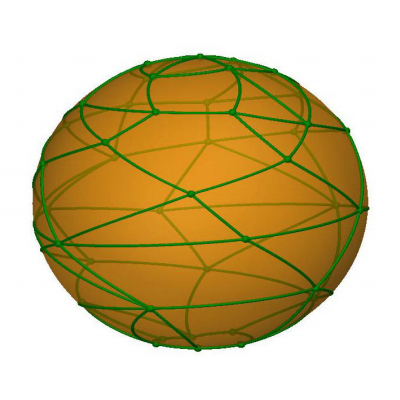
Uma informação importante sobre uma superfície é sua característica de Euler (χ), que pode ser obtida de qualquer subdivisão da superfície em polígonos. Contando-se faces (F), arestas (A) e vértices (V) da subdivisão, calcula-se o número χ=F−A+V. É possível mostrar que esse número não depende da subdivisão escolhida. A esfera, por exemplo, tem característica de Euler igual a 2, e é por isso que todos os poliedros convexos satisfazem a fórmula de Euler.