CENTRO DE MASSA DE FIGURAS PLANAS
Indicaremos duas maneiras de determinar o centro de massa de placas a partir de suas propriedades físicas.
Para a primeira, pendure a figura em um pino. Em seguida, use o fio de prumo para marcar uma reta vertical na placa. Repita o processo pendurando a placa em outra posição. Pronto, o cruzamento das duas retas é o centro de massa!

A segunda usa uma placa de metal para equilibrar a figura em duas posições diferentes, marcando a posição da placa metálica. Novamente, o cruzamento das retas é o centro de massa!

No entanto, o centro de massa também pode ser determinado matematicamente, com base apenas na forma da placa (supondo que ela seja homogênea). Para uma placa triangular, por exemplo, é o ponto de encontro das medianas, isto é, o baricentro do triângulo. Para uma placa poligonal, ele pode ser determinado decompondo o polígono em vários triângulos e então ponderando os centros de massa de cada um por suas áreas.
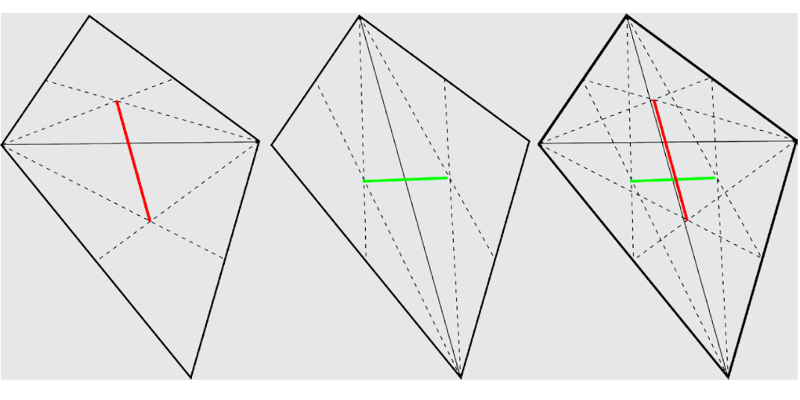
Na figura abaixo vemos 3 cópias de um quadrilátero. Na primeira, dividimos em dois triângulos e achamos seus baricentros pelo encontro de duas medianas. O segmento vermelho entre os dois baricentros deve conter o centro de massa da placa. Fazemos o mesmo com outra divisão em triângulos e daí tiramos que o centro de massa está no segmento verde. Conclusão: o centro de massa é a intersecção dos segmentos verde e vermelho.