POLIEDROS FLEXÍVEIS
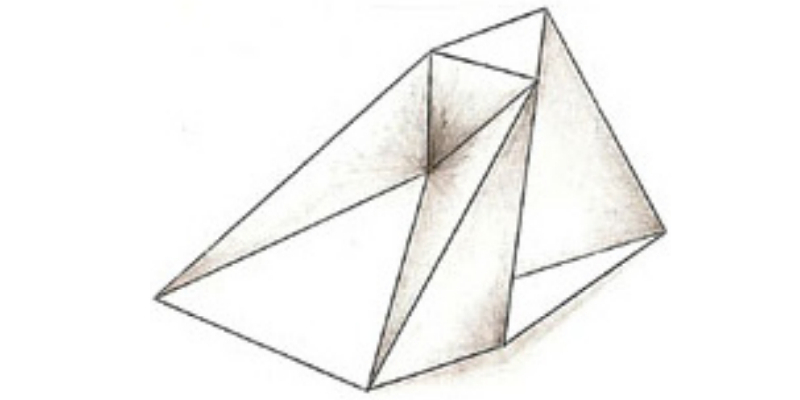
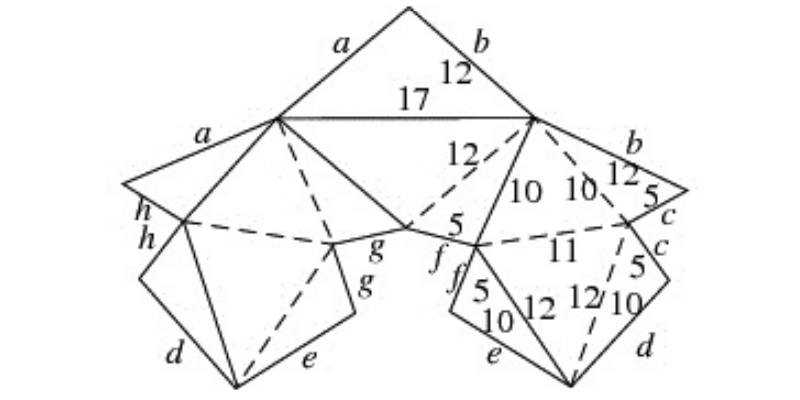
O poliedro que aparece na figura é flexível!! As faces são rígidas e as arestas flexionam como se fossem dobradiças.
Isto pode não surpreender à primeira vista, mas é uma conquista recente da geometria. Em 1813, Cauchy provou que um poliedro convexo não pode ser flexível, mas ficou a pergunta se isso seria possível com poliedros não convexos.
Foi somente em 1977 que Robert Conelly encontrou o primeiro exemplo de um poliedro não convexo e flexível. O objeto que apresentamos aqui foi criado por Klaus Steffen alguns anos depois.
Um problema recentemente solucionado foi a chamada conjectura do fole: especulava-se que um poliedro flexível deveria ter volume constante. A resposta positiva a esta conjectura foi dada por Conelly em 1997. Em termos concretos, significa que, se abrirmos um buraco em uma das faces, o movimento do poliedro nem expelirá nem sugará ar, daí o nome da conjectura.