SIMETRIAS
Esses aparatos nos permitem brincar com os grupos de rotação de vários objetos: bolas esportivas, poliedros, etc.

A ordem do eixo de simetria é o número n de vezes que o objeto volta à mesma configuração até completar uma volta. A cada giro de 360/n, a peça volta à mesma configuração.
Perceba que as bolas esportivas têm diferentes configurações de eixos de simetria. Por outro lado, algumas bolas com desenhos diferentes entre si têm exatamente a mesma configuração de eixos. De fato, seus grupos de simetria de rotação são idênticos, embora seus desenhos não o sejam.
Além das bolas esportivas, outro objeto em que podemos ver facilmente as simetrias é o cubo! Bom.. ele parece bem simétrico, né? Será que podemos medir a quantidade de simetria de alguma forma?
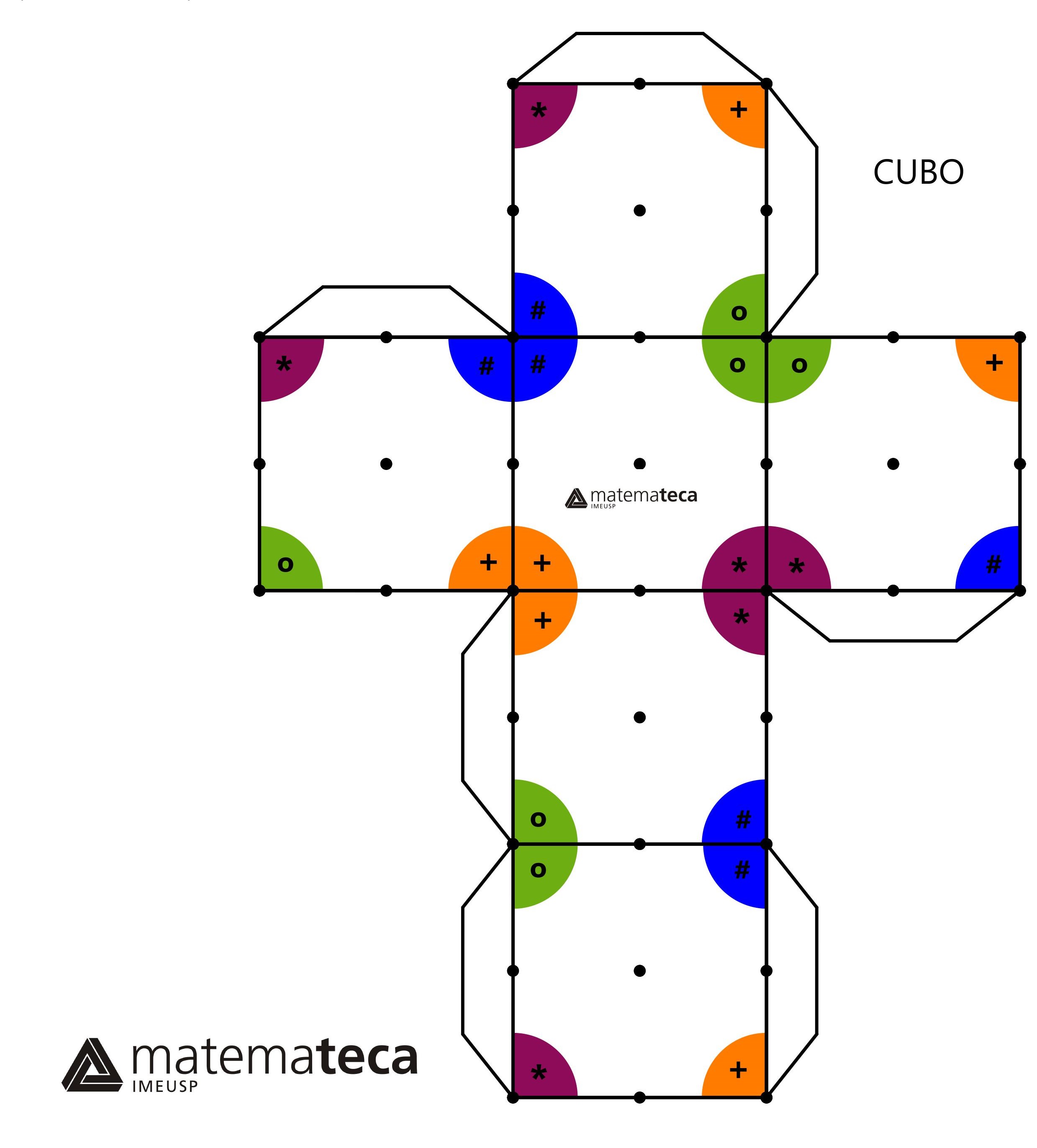
De quantas maneiras distintas podemos movimentar um cubo de forma que ele sempre ocupe o mesmo lugar no espaço? Usando os cubos com as diagonais marcadas, é possível verificar que cada movimento desse tipo corresponde a uma troca na posição das diagonais. Esse é o primeiro passo para perceber que cada simetria do cubo corresponde a uma permutação distinta entre as 4 diagonais e vice-versa. Ou seja, no grupo das simetrias do cubo temos 24 (ou 4!) elementos.

Aliás, é possível improvisar esse cubo espetado com o seguinte modelo, a partir das instruções a seguir. Se preferir, pode baixá-lo por este link.
1: Imprima em papel de alta gramatura (ex. 180g/m2) ou cartolina, ou então imprima em papel comum e cole sobre uma cartolina.
2: Coloque um papelão por baixo e fure com uma tachinha nos pontos marcados. Com um palito de churrasco, alargue os furos de modo que o palito passe justo e suavemente. Recorte a figura.
3: Com a ajuda de uma régua, dobre as arestas e as abas. Monte o poliedro com a parte impressa para fora, colocando as abas (as abas ficam no interior do poliedro; não as dobre demais para permitir um pouco de pressão na hora da colagem). Espere secar bem.
4: Com o palito de churrasco, reforce os furos, atravessando o poliedro nos eixos de simetria. Não alargue os furos demais, para facilitar o giro do poliedro apenas pela manipulação do palito.
OBS: As cores podem ser referenciadas por suas letras (R = roxo, L = laranja, A = azul, V = verde) ou pelos símbolos correspondentes.
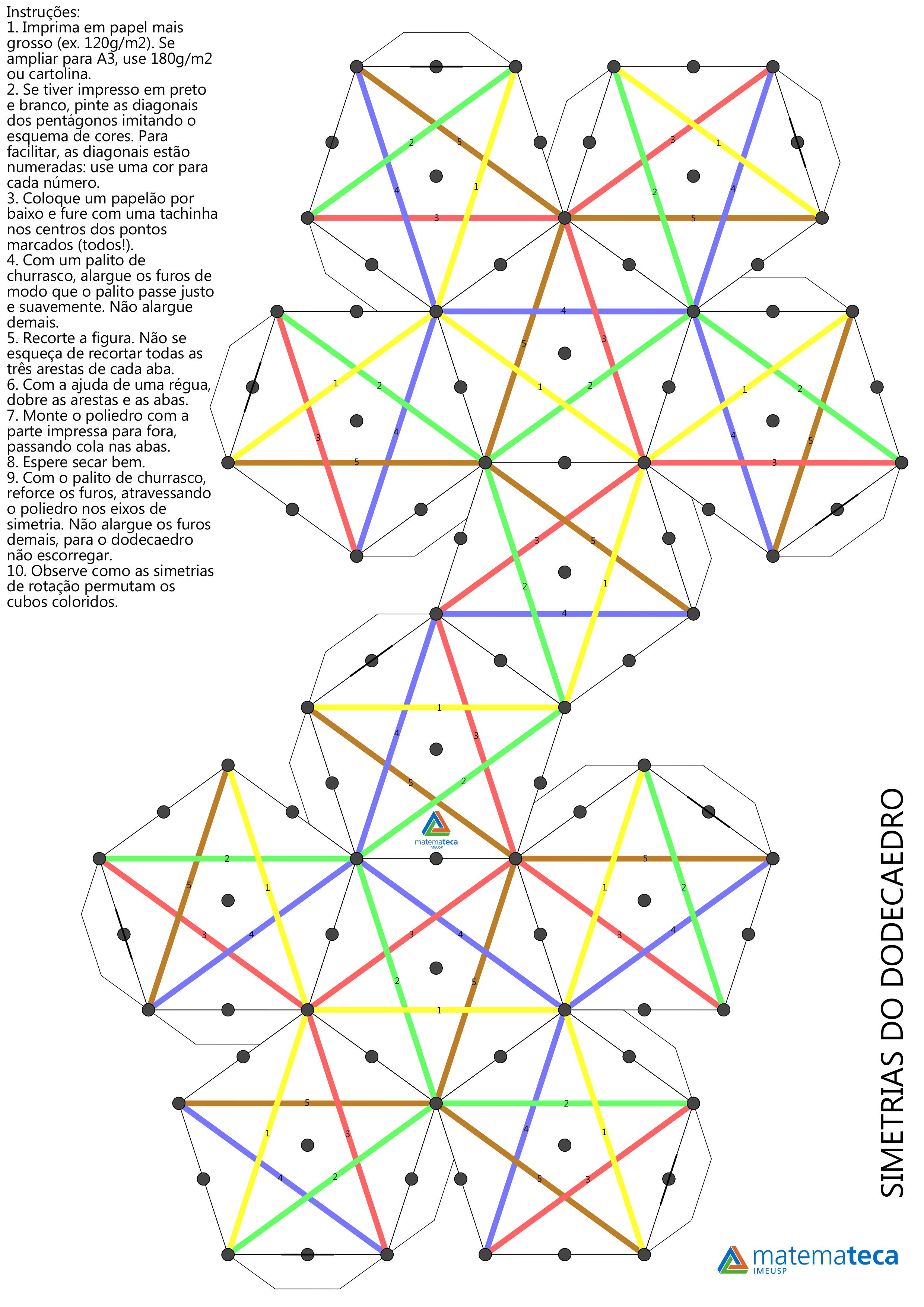
E como será que são as simetrias de outros sólidos platônicos? Abaixo, temos imagens de alguns exemplos: as simetrias do dodecaedro, do prisma triangular e do tetraedro, os quais também podem ser acessados como PDF clicando nos links acima.
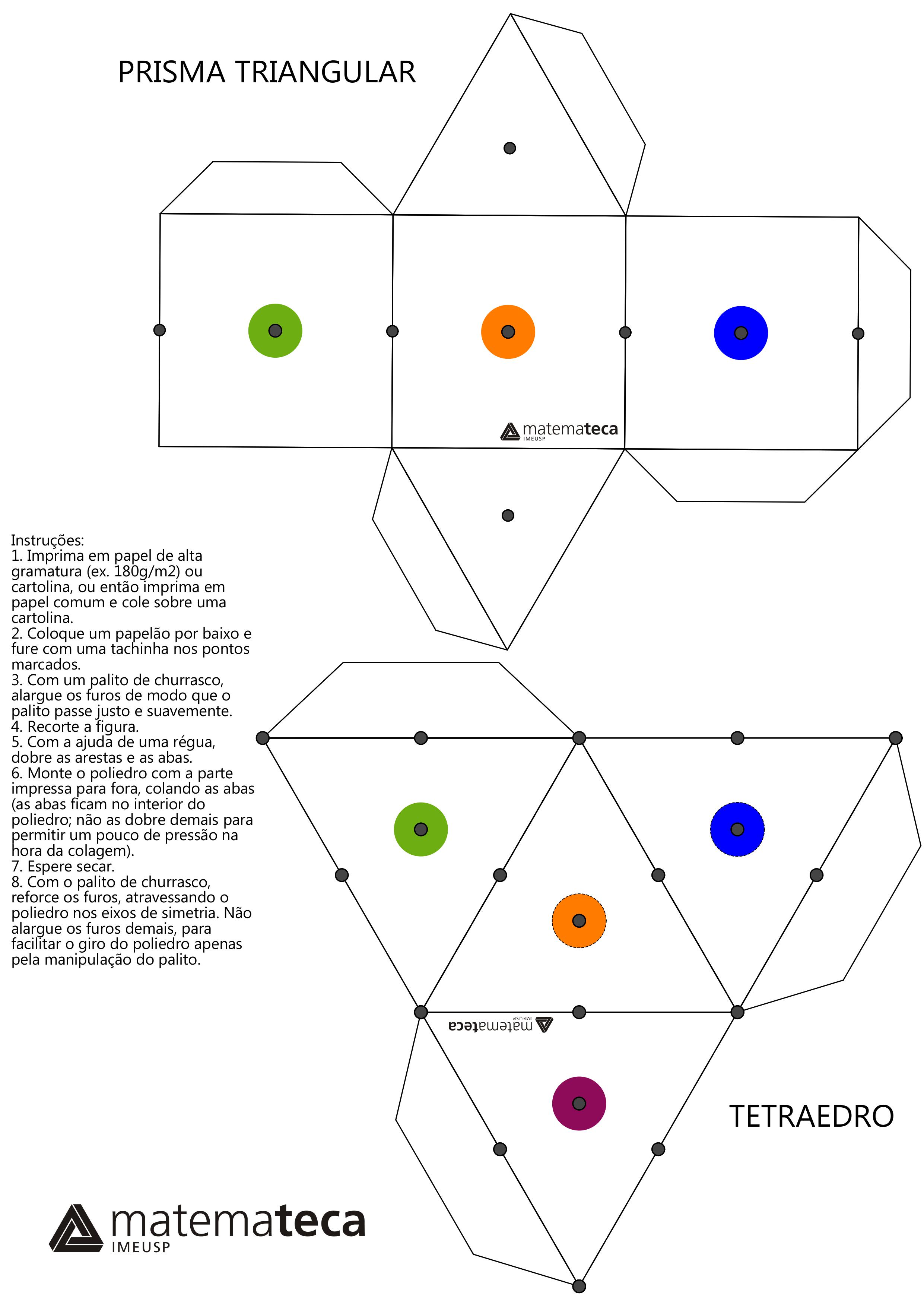
Se você suspeita que o objeto tenha um eixo de simetria rotacional, coloque-o numa das plataformas com esse eixo na vertical e coloque uma cópia do objeto na plataforma ao lado, na mesma posição, para comparação. Se for possível girar o objeto em menos de 360 graus de tal modo que ele volte à configuração inicial, então a suspeita se confirmou: esse eixo é realmente um eixo de simetria rotacional.

Para descobrir ainda mais sobre esse assunto, basta dar uma olhada nos vídeos abaixo! Aproveite e confira os outros vídeos bem legais que tem no canal da Matemateca!
