TABULEIRO DE GALTON OU QUINCUX

Este experimento serve, em primeira aproximação, para ilustrar a chamada distribuição binomial.

Colocando a peça “de cabeça para baixo”, todas as bolinhas cairão. Veja sua distribuição.

Se em cada pino a probabilidade de ir para a direita ou para a esquerda for igual, lá embaixo as bolinhas vão se distribuir de forma proporcional aos coeficientes da expansão de (a + b)n, que é o binômio de Newton (no experimento, n = 9).

Por exemplo,
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
tem coeficientes 1, 4, 6, 4 e 1.

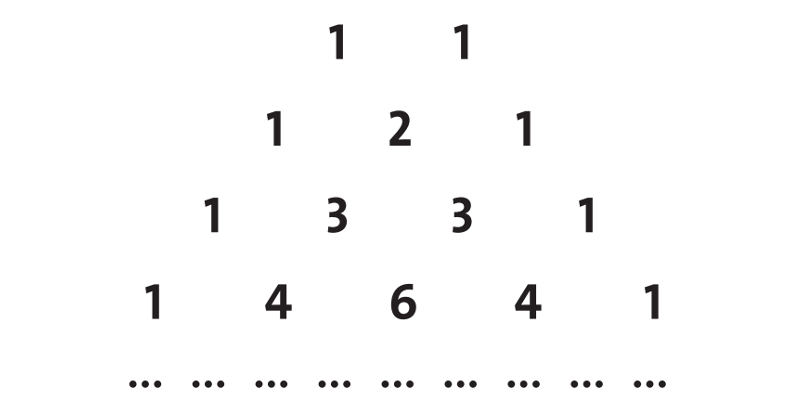
Os coeficientes de (a + b)n podem ser obtidos de forma fácil na n-ésima linha do triângulo de Pascal(ver figura abaixo). Exceto nas pontas, cada número de uma linha é obtido como a soma dos dois elementos da linha anterior que lhe são mais próximos.

Triângulo de Pascal até n = 4.

No entanto, não é difícil notar que os parâmetros envolvidos no experimento, como o raio dos pinos e bolinhas, a distância entre os pinos, a elasticidade dos choques etc, podem influenciar o resultado (pense, por exemplo, que se os pinos estivessem muito afastados, então todas as bolas cairiam no meio). Isto mostra a necessidade de uma modelagem mais apurada.

Se quiser ver um pouco mais sobre esse jogo, dê uma olhada no vídeo abaixo! Aproveite e confira os outros vídeos bem legais que tem no canal da Matemateca!

                 

LINKS ÚTEIS

Nesta página do iMática você vai encontrar mais explicações sobre a distribuição binomial, o triângulo de Pascal, e um simulador do tabuleiro de Galton para brincar!




Esta página da Wikipedia discorre sobre o Tabuleiro de Galton, também chamado de Quincunx. Nela, temos a descrição do funcionamento da máquina e da distribuição das bolinhas, a qual tem a ver com a distribuição binomial. Também há um breve comentário sobre a sua história.

Este vídeo do canal Four Pines Publishing é um documentário sobre o Tabuleiro de Galton e como ele foi construído como objeto para que se estudasse a distribuição normal, tão presente na maioria dos estudos de variáveis quantitativas. É um vídeo bastante interativo, com diversas imagens, comparações e falas de alguns estudiosos.

Esta página do Math is fun possibilita que os internautas simulem o Tabuleiro de Galton, podendo escolher o tamanho do tabuleiro, isto é, a quantidade de linhas, a qual varia de 1 a 15, a velocidade das bolinhas e a probabilidade de ela ir para a direita ou para a esquerda. Se a configuração de 50% / 50% não for alterada, é o Tabuleiro original, já que a probabilidade é a mesma em um tabuleiro bem construído.

Por fim, este artigo de uma aluna da Universidade Estadual de Campinas traz o estudo da distribuição binomial utilizando o Tabuleiro de Galton. Nele, há uma montagem artesanal do Tabuleiro e um estudo das probabilidades bastante aprofundado, com conceitos estatísticos mais precisos. São apresentados os resultados experimentais e um estudo deles e das incertezas envolvidas.