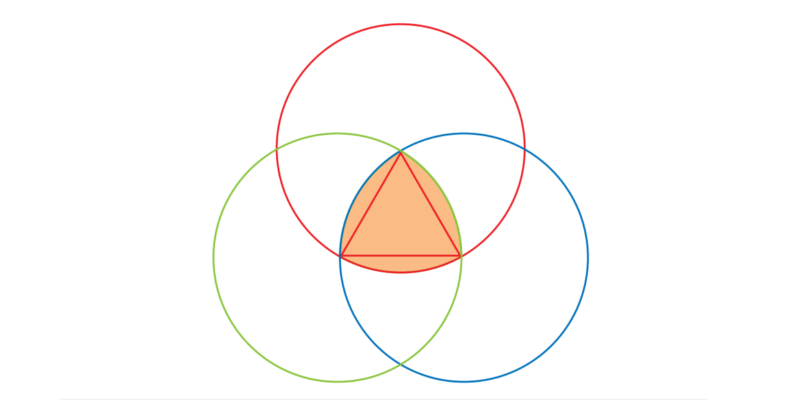
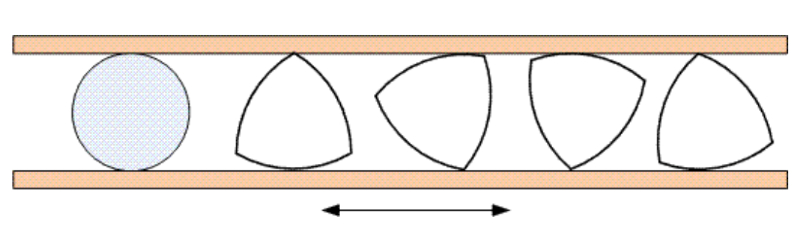
TRIÂNGULO DE REULEAUX
Uma figura plana de largura constante tem a seguinte propriedade: sempre que nela encostamos duas retas paralelas de forma a cercá-la, a distância entre as retas é constante. Além do círculo, o exemplo mais simples é o Triângulo de Reuleaux, que apresentamos aqui.